科里奥利加速度的简单理解

之前在极坐标分解中，横向加速度 $\vec a_\theta = (2\frac{dr}{dt}\frac{d\theta}{dt}+r\frac{d^{2}\theta}{dt^{2}})\vec e_\theta$，其中的 $2\frac{dr}{dt}\frac{d\theta}{dt}$ 也就是科里奥利加速度一直没完全理解，这几天翻看力学教材的时候貌似想通了。

---

实际上，对于平面转动参考系，我们采用平面极坐标可以更加方便地理解。
如图我们在转动中心处建立极坐标

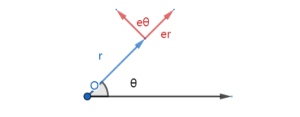
有 $\vec{e_r} = cos\theta\vec{i}+sin\theta\vec{j}$;$\vec{e_\theta} = -sin\theta\vec{i}+cos\theta\vec{j}$
将 $\vec{e_r}$ 对 $\theta$ 求导有 $\frac{d\vec{e_r}}{d\theta}=-sin\theta\vec{i}+cos\theta\vec{j}=\vec{e_\theta} $;
将 $\vec{e_\theta}$ 对 $\theta$ 求导有 $\frac{d\vec{e_r}}{d\theta}= -cos\theta\vec{i}-sin\theta\vec{j}=-\vec{e_r} $
很容易得到径向速度 $\vec{v_r}=\frac{dr}{dt}\vec{e_r}$，横向速度$\vec{v_\theta}=r\frac{d\theta}{dt}\vec{e_\theta}$
所以合速度 $\vec{v}=\dot{r}\vec{e_r}+r\dot{\theta}\vec{e_\theta}$（下面为了表示方便将对时间求一阶导数以上方加一点表示，二阶导数以上方加两点表示），那么加速度便有
$\vec{a}=\frac{d\vec{v}}{dt}=\ddot{r}\vec{e_r}+\dot{r}\dot{\vec{e_r}}+\dot{r}\dot{\theta}\vec{e_\theta}+r\ddot{\theta}\vec{e_\theta}+r\dot{\theta}\dot{\vec{e_\theta}}$
$=\ddot{r}\vec{e_r}+\dot{r}\frac{d\vec{e_r}}{d\theta}\frac{d\theta}{dt}+\dot{r}\dot{\theta}\vec{e_\theta}+r\ddot{\theta}\vec{e_\theta}+r\dot{\theta}\frac{d\vec{e_\theta}}{d\theta}\frac{d\theta}{dt}$
$=\ddot{r}\vec{e_r}+\dot{r}\dot{\theta}\vec{e_\theta}+\dot{r}\dot{\theta}\vec{e_\theta}+r\ddot{\theta}\vec{e_\theta}-r\dot{\theta}^{2}\vec{e_r}$
$=(\ddot{r}-r\dot{\theta}^{2})\vec{e_r}+(2\dot{r}\dot{\theta}+r\ddot{\theta})\vec{e_\theta}$
于是横向加速度${a_\theta}=2\dot{r}\dot{\theta}+r\ddot{\theta}$

那么横向加速度上的 $2\dot{r}\dot{\theta}$ 也就是 $2\frac{dr}{dt}\frac{d\theta}{dt}$ 应该如何理解呢？

---

先引用一下百度词条对科里奥利加速度的描述：

科里奥利加速度（Coriolis acceleration），又名科氏加速度，在转动参考系中，物体在做牵连运动的同时，沿旋转半径做相对运动，由牵连运动和相对运动交互耦合而形成的加速度称为科里奥利加速度。

我第一次看到这段对科里奥利加速度（以下简称科氏加速度）的描述，仅仅只是知道他是存在于转动参考系中的，而当我看到上文所提到的 $2\frac{dr}{dt}\frac{d\theta}{dt}$ 时，更加是不知所云。径向速度 $\frac{dr}{dt}$ 乘角速度 $\frac{d\theta}{dt}$？前面的2又是代表着啥？而今天在翻看教材惯性力部分时，将一个转动参考系画在纸上时，方才恍然大悟。

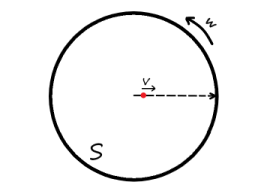
如图所示我们设一转动参考系S，该参考系角速度朝向屏幕外侧且大小为 $\omega$，在S系下有一小球（红色圆形表示）正在伴随着S一同转动的同时，相对S由S的转动中心沿着某一半径以速度$v$向外侧做匀速径向直线运动。我们也知道在我们的静止参考系中，小球正做着螺旋线运动，而且在静止参考系看来该小球的运动规矩正好是一条阿基米德螺线，当然这不是我们分析的重点。
回到S系中，我们的小球正在向外侧运动，小球的转动半径在不断增加，又因为小球有着与S系相同的角速度 $\omega$，那么此刻小球的切向速度正在伴随着转动半径的增加而增大，先设小球切向速度为$v’$，转动半径为$r$，那么很容易得到$v’=\omega·r$，所以我们可以得到小球在切向的加速度便为$a_1=\frac{dv’}{dt}=\frac{d\omega·r}{dt}=\omega\frac{dr}{dt}=\frac{dr}{dt}\frac{d\theta}{dt}$
但是我们发现这里我们仅仅只是得到了一个 $\frac{dr}{dt}\frac{d\theta}{dt}$，而在公式中我们却是 $2\frac{dr}{dt}\frac{d\theta}{dt}$，那这个二倍是怎么回事呢？
其实我们在上面仅仅只是考虑了小球相对于转动的S系由于向外运动产生的切向加速度，而实际上对于静止参考系的我们来说小球还伴随着S系旋转了一段微小角度$d\theta$

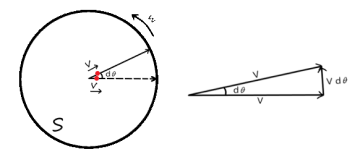
于是我们的小球还存在一个径向速度的变化量$dv’’=vd\theta$。所以还存在一个加速度 $a_2=\frac{dv’’}{dt}=\frac{vd\theta}{dt}=\frac{dr}{dt}\frac{d\theta}{dt}$

综上所述，科氏加速度的一部分是由于沿旋转半径做相对运动产生的$a_1$，以及另一部分由于牵连转动产生的$a_2$，两者相互耦合而成的，所以我们的科氏加速度$a_{Cor}=2\frac{dr}{dt}\frac{d\theta}{dt}=2\omega v$便得出来了。