基于共振原理的“不倒的杆”简单结构设计
题目 1:不倒的杆
目的:
1)研究物体/装置的平衡原理;
2)制作一个能够帮助杆在风力等作用下稳定不倒的实际应用装置或实验研究装置。
要求:
1)设计实验方案(含原理);
2)制作一个实验装置,实现杆在风力等作用下的稳定不倒;
3)给出实验结果,量化抵御外部作用的能力,讨论不确定度。
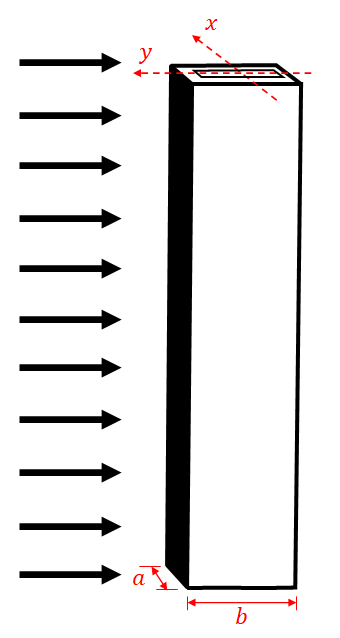
对于风力作用下的杆,由于顺风向的脉动风荷载将使得杆结构在顺风方向产生受迫振动。考虑在微小幅度振动下,初步研究先不记其重力对振动的影响,且先考虑单一风向均匀分布的风荷载,因此可将模型初步简化成杆受单侧变化均布荷载的作用下的振动。在不记重力影响的情况下可进一步将模型简化类比为仅有一固定端约束的简支梁在均布荷载下的受力分析。
欲研究杆的共振,则需先得到杆的固有频率,下面将计算固有频率:
单独对该杆在无阻尼自由振动下研究,对于如下杆模型,取广义坐标$\delta$,则有,
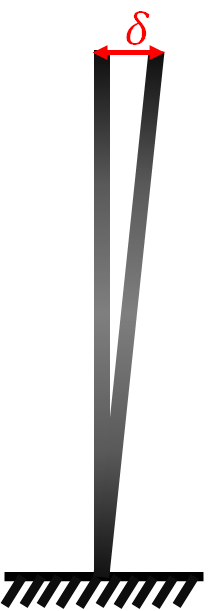
$
\begin{cases}
T=\frac{1}{6}m\dot{\delta}^2\
V=E_{pG}(\delta)+E_{pK}(\delta)\
\end{cases}
$
其中$E_{pG}$为杆的重力势能,$E_{pK}$,为振动过程中储存在杆内的“弹性势能”,取杆在静止时的重力势能为零,忽略振动过程中重力势能的变化,则得到拉格朗日函数,
$$
L(\delta)=T-V=\frac{1}{6}m\dot{\delta}^2-E_{pK}(\delta)
$$
求解拉格朗日方程,
$$
\frac{d}{dt}(\frac{\partial L}{\partial \dot{\delta}})-\frac{\partial L}{\partial \delta}=0 \
\Rightarrow \frac{1}{3}m\ddot{\delta}+\frac{d E_{pK}(\delta)}{d\delta}=0
$$
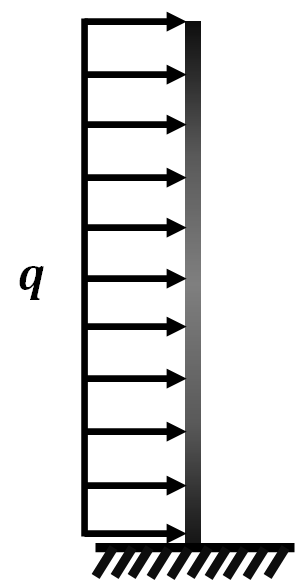
因此想要得到杆的固有频率需要找到振动过程中由于杆的弯曲储存在杆内的能量,上面提到我们可以把杆模型类比成均布荷载下仅有一固定端约束的简支梁。
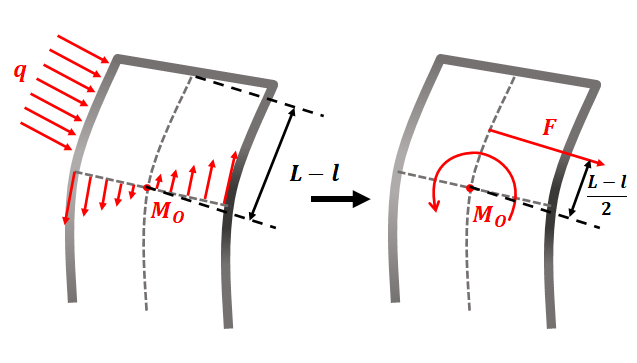
那么杆的弯曲在每一时刻产生的弯曲储存的能量等同于施加某一大小的均布荷载对使杆弯曲到这一弯曲形态下荷载所做的功,任取杆上一段弯曲分析。
设杆总长为$L$,对于杆$l$处截面$O$由于杆的弯曲,取上端杆分析,下端杆在左侧对上端杆产生拉力,在右侧对上端杆产生压力,从而形成一对力偶,其力偶矩$M_{O}$和作用在上端杆的均布荷载产生的力矩$M_{q}$平衡,有,$M_{q}=M_{O}$,其中$M_{q}$可看作分布荷载作用在上端杆长度中心处的集中力产生的力矩,则有,
$M_{q}=\frac{1}{2}q{(L-l)}^{2}$
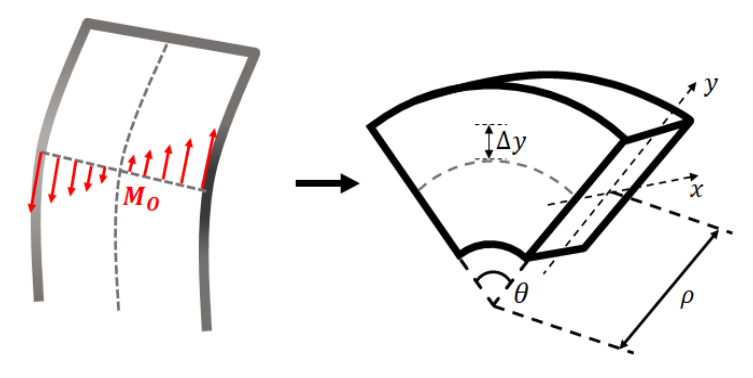
接下来讨论$M_{O}$的表达式。如图4,在$O$截面附近截取一段弯曲的杆,设中性面长度(该杆弯曲前原长)$l_{0}$,弯曲角度为$\theta$,弯曲曲率半径为$\rho$,则可以写出下式,
$$
\frac{\Delta l_{0}}{l_{0}}=\frac{(\rho +y)\theta -\rho\theta}{\rho\theta}=\frac{y}{\rho}
$$
根据材料弹性模量$E$的定义,有$E=\frac{\sigma}{\varepsilon}=\frac{F/S}{\Delta l_{0}/l_{0}}$
则,
$$
\begin{aligned}
dF&=ES\cdot \frac{y}{\rho }\
=E\frac{y}{\rho }dydx
\end{aligned}
$$
所以,$dM=ydF=E\frac{y^{2}}{\rho }dydx$
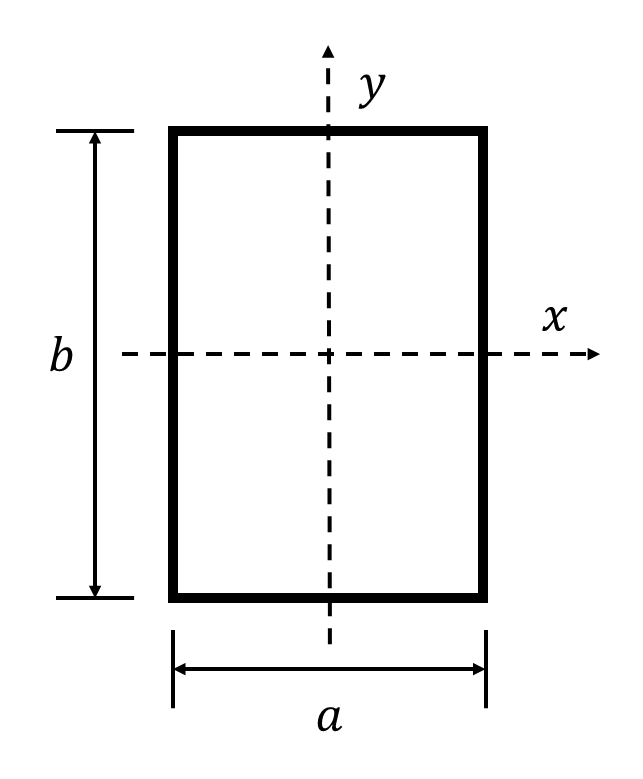
对于宽$a$长$b$的截面有
$$
M=\frac{E}{\rho}\int_{-\frac{b}{2}}^{\frac{b}{2}}{\int_{-\frac{a}{2}}^{\frac{a}{2}}{y^{2}}dxdy} \
=\frac{1}{12}\frac{E}{\rho}a{b^{3}}
$$
又有曲率半径$\rho =\frac{(1+y^{‘2})^{\frac{3}{2}}}{y^{‘’}}$,在小段弯曲上${y}^{‘2}<<1$,有$\rho =\frac{1}{y^{‘’}}$,则,
$$
M_O=M=\frac{1}{12}Ey^{‘’}a{b^{3}}
$$
回到$M_{q}=M_{O}$,加上初始条件$y’(0)=0; y’’(0)=0$便得到,
$$
\frac{1}{2}q{(L-l)^{2}}=\frac{1}{12}Ey^{‘’}a{b^{3}}
\Rightarrow y^{‘’}=\frac{6q{(L-l)^{2}}}{Ea{b^{3}}}
\Rightarrow y(l)=\frac{q{l^{2}}}{2Ea{b^{3}}}(6{L^{2}}-4Ll+{l^{2}})
$$
则
$$
dW=qdl\cdot y \Rightarrow W=\int_{0}^{L}qydl \
=\frac{q^{2}}{3Ea{b^{3}}} \int_{0}^{L}(6{L}^{2}-4Ll+l^{2})l^{2} \
=\frac{4}{15}\frac{q^{2}L^{5}}{Eab^{3}} \
$$
又因为
$$
\delta = y(L)= \frac{3qL^{4}}{2Eab^{3}}
$$
则
$$
\begin{cases}
\delta = \frac{3qL^{4}}{2Eab^{3}}\
W = \frac{4}{15}\frac{q^{2}}{L^{5}}Eab^{3}\
\end{cases}
\Rightarrow W= \frac{16Eab^{3}}{135L^{3}}{\delta ^{2}}
$$
于是,便得到了$E_{pK}$关于$\delta$表达式,即
$$
E_{pK}(\delta)= \frac{16Eab^{3}}{135L^{3}}{\delta ^{2}}
$$
所以杆在单侧均布荷载的作用下振动的运动微分方程可以写成
$$
\frac{1}{3}m\ddot{\delta}+\frac{d E_{pK}(\delta)}{d\delta}=0
\Rightarrow \frac{1}{3}m\ddot{\delta}+\frac{32Eab^{3}}{135L^{3}}=0
$$
则其固有频率为
$$
\begin{aligned}
{\omega _{0}} =\sqrt{\frac{32Eab^{3}/135L^{3}}{m/3}} \
=2\sqrt{\frac{Eab^{3}}{5mL^{3}}} \
\end{aligned}
$$
可以看出一个均匀质量的杆在均布荷载作用下形变(因为不同荷载下杆形变不同以至于$E_{pK}$的表达式不同,现在先考虑均布荷载情况)的固有频率和杆长$L$、截面的参数$a$、$b$有关以及材料的弹性模量$E$有关。于是要降低杆发生共振的几率,可以想办法提高杆的固有频率来应对不同脉动频率的风荷载,从上述表达式看,提高固有频率可以通过:
(1)降低重心(减小有效长度$L$);
(2)寻找一个合适的截面;
(3)使用刚度更强的材料。
现在开始寻找解决方案:
一、降低杆的重心
通过上面固有频率的表达式$\omega_{0}=2\sqrt{\frac{Eab^{3}}{5mL^{3}}}$可以看到杆越短其固有频率越大,但是很明显仅仅通过缩短杆的长度并不现实,但是我们可以通过减小杆子的有效长度也就是保持杆子长度而降低杆子的重心来达到相同的效果。
降低杆的重心有很多途径,比如我们可以在杆的下段采用密度较大的的材料或者我们可以使用相同材料但是将杆的下端做粗等等。综合杆的一体性,为了方便制作出成品,我们采用做一个下端粗上端细的杆的方案。
这样以来杆的重心下降,不仅仅可以增加其固有频率,同时在杆受风倾斜角度较大时,重力对杆的影响就难以忽略了。这时如果在杆子的质量不变的情况下,重心越低,根据$\vec{M}=\vec{r}\times\vec{F}$,重力对转轴的力矩就越小,杆就越不容易因为受到重力的影响而倒下。如果制作的更为极端,单从降低重心的角度来看,杆子埋入固定处较深时,我们可以认为杆子倾倒时,整体可以看作绕固定点定轴转动,固定点类似转动过程中的稳心,这时如果杆子的重心下沉到稳心以下,重力对转轴的力矩反而可以进一步削弱风在固定点上端作用力对转轴的力矩,进一步削弱杆的倾倒。
二、寻找一个合适的截面
从先前固有频率的推导看,
$$
M=\frac{E}{\rho}\int_{-\frac{b}{2}}^{\frac{b}{2}}{\int_{-\frac{a}{2}}^{\frac{a}{2}}{y^{2}}dxdy} \
=\frac{1}{12}\frac{E}{\rho}a{b^{3}}
$$
式中积分的过程对于均质杆实际上等同于在求转动惯量关于$y$轴的惯性矩。设$I_{x}=\int_{S}{y^{2}dS}$,那么有,
$$
\begin{aligned}
M&=\frac{E}{\rho }\int_{S}{y^{2}dS} \
\end{aligned}
$$
进一步按照上面的方法推导,可以得到$\omega_{0}=12\sqrt{\frac{EI_{x}}{5mL^{3}}}$
所以我们的截面需要选择一个对于$x$轴具有较大惯性矩的截面,由$I_{x}$的表达式$I_{x}=\int_{S}{y^{2}dS}$,很容易看出,当截面上的点越远离$x$轴,$I_{x}$的值越大,这样一来$\omega_{0}$便越大,越不容易产生共振。对于相同的截面面积,要让截面上的点远离$x$轴,可以采用:(1)将迎风面($y$方向)做窄;(2)将中心部分挖空,即做成空心环状截面。
现在我们只考虑了迎风面的振动,但实际上在杆的侧面也会产生振动,和直接由一些频率的脉动风荷载激励的振动不同的是,侧面的振动是由于风流经杆后产生的涡街导致的,而相比与迎风面的共振,侧面的涡激共振产生的破坏性更大,著名的美国塔科马悬桥风毁事件的元凶便是涡激共振。
考虑在侧面涡激振动便要进一步寻找侧面方向杆的固有频率,简化问题的情况下和上方迎风面求固有频率类似,但是固有频率公式中的惯性矩将由$I_{x}$变成$I_{y}$,即,
$w_{0’}=12\sqrt{\frac{EI_{y}}{5mL^{3}}}$
因此为了寻找更好的截面,还要综合涡激振动
涡街振动频率公式,$f_{t}=\frac{S_{t}V}{a}$
其中$S_{t}$为斯特劳哈尔数,$V$是风速,$a$为迎风面的有效宽度,在一定的条件下,我们可以认为$S_{t}$为一个常数,这样侧面的涡激振动频率可以看作正比于风速和迎风宽度的倒数的乘积,即,$f\propto V\cdot {a^{-1}}$
为了提高顺风方向的固有频率,我们需要把迎风面做得相对较窄,但是为了降低涡激振动的频率,我们似乎又不能让迎风面变得太窄,这样一来单从一个截面同时考量顺风方向由脉动风引起的振动和,侧面涡激振动似乎存在一定的困难,于是我们选择从杆整体分析。
首先为了减小涡街的产生,我们需要一个具有弧度的表面,这样一来我们初步得到了一个,截面为一个空心圆环的杆体。由于变化迎风面的宽度和降低涡激振动的频率之间存在较为复杂的联系,我们决定在整体方面减小涡激振动,我们的解决方案决定在圆环的基础上将截面变为椭圆圆环,为了减小涡激振动,我们反过来利用不同方向的涡激振动,让截面成为一个至上而下旋转的空心椭圆环,使不同高度截面由于不同弧度产生的不同方向的涡街脱落相互制约以达到从整体上减小涡激振动。改进过程参照图7。
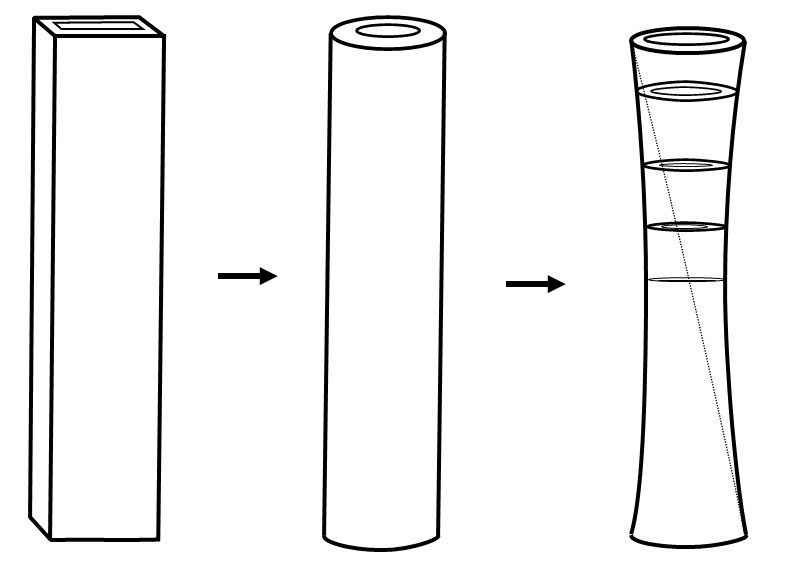
对于材料的选择不在我们的考虑范围,那么综合上述改良我们得到的最后方案是一个下粗上细,截面为至上而下旋转的空心椭圆环的杆体,如图8。
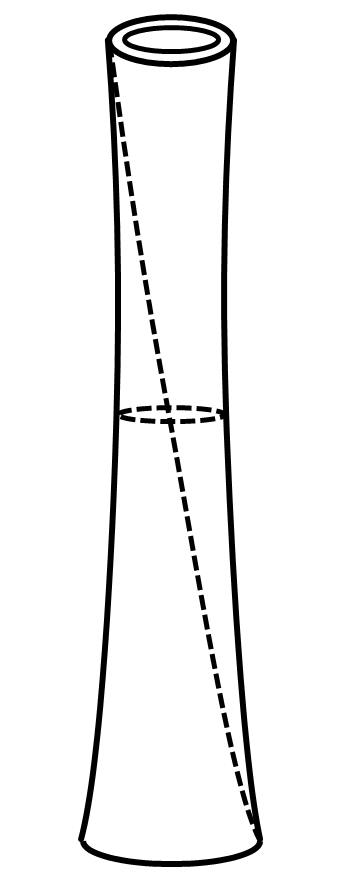
现在我们已经得到了杆子的基本结构,但单单是这样一个杆结构是很难保障杆能在风力作用下而不易倒下。同样可以从减小共振发生的概率的角度出发,为了防止在风力作用下杆的振动达到其共振频率,我们可以在振动的过程中添加阻尼,防止振动的频率过大。
现实生活中,有很多过高的建筑都需要做防风设计,其中许多高层建筑额外安装了叫做“调谐质块阻尼器(TMD)”,俗称“风阻尼器”的仪器,其工作原理是通过将阻尼器的频率调整至和建筑的固有频率相当,当风力作用下建筑被激励振动时,风阻尼器会由于惯性等其他因素(对于不同种类的阻尼器其工作方式有一定的差别)产生的回复力使得阻尼器与建筑体振动方向相反,在振动过程中,建筑体的动能一部分被阻尼器耗散掉从而减小建筑体的振动。